Building a regex engine

, ,

Introduction

Regular expressions, commonly known as regex are something that every developer might have used at some point. They’re really powerful tools for finding patterns in text, but they can often seem confusing and hard to read, especially if they are just being copy-pasted. In this blog, we’ll explore how regex engines actually work under the hood. Here, we’ll build a simple regex engine from scratch in C++ using basic concepts. In the upcoming posts, we’ll look at how to optimize the regex engine we’re building, using some powerful algorithms and concepts.

Regular expressions and languages

A language is nothing but a set of strings (i.e. sequences of symbols from an alphabet) that can be described using regular expressions. Regular expressions are patterns made up of characters, used to find or match specific parts of a string. They’re built using a few basic operators that let us combine simple patterns to form more complex ones. In other words, larger regular expressions can be built by putting together smaller, simpler ones.

Consider a regular expression r that defines a language L(r). Then, L(r) is the set of all strings that match the regex r. Before we dive into operators, there’s one special symbol that will play a crucial role in building our regex engine. It’s epsilon (ε), a symbol that represents the empty string.

Operators

Now we’ll see how larger regular expressions can be built from smaller ones. Consider two regular expressions r1 and r2. The fundamental operators used to combined these expressions are:

  1. Union:
    The union operator allows you to choose between two expressions. It means either the left side or the right side. For example, r1 | r2, the union of r1 and r2 is a regular expression denoting the language L(r1) ∪ L(r2) i.e. L(r1|r2) = L(r1) ∪ L(r2).

  2. Concatenation:
    It refers to the operation of combining two or more regex patterns sequentially. For example, r1r2 denotes the concatenation of regular expressions r1 and r2, and L(r1r2) = L(r1)L(r2).

  3. Kleene closure:
    It allows zero or more repetitions of a pattern i.e. L(r*) = {ε} ∪ L(r) ∪ L(rr) ∪ L(rrr) ∪ ....

An example of a regular expression created using these operators is (a|b)*ab. Few strings that match this regex are ab, aab, bab, aaab, bbab, aaaab, and so on.

Finite Automata

So far, we’ve seen how regular expressions can describe languages using just a few simple operations: union, concatenation, and Kleene closure. But how do we go from these definitions to actual stuff that can recognize whether a given string belongs to the described language? That’s where finite automata come into play. A finite automaton is a mathematical model of computation that’s used to recognize patterns in strings. It simply decides whether to accept or reject a string. There are two types of finite automata: non-deterministic and deterministic. In this post, we’ll only cover NFA (Non-deterministic finite automata). DFA (deterministic finite automata) shall be discussed in upcoming posts.

Non-deterministic finite automata

An NFA is a machine that processes input strings by moving (transitioning) between states based on the symbols it reads. It accepts a string if there’s at least one path that leads to an accepting state.

Mathematically, an NFA is defined as N=(Q,Σ,δ,q0,F)
where,

  • Q represents a finite set of states.
  • Σ represents the input alphabet (a finite set of symbols).
  • δ (also known as move) represents the transition function, which determines the possible next states given a current state and an input symbol i, where i ∈ (Σ ∪ ε). Please note that state transitions can also occur without consuming any input symbol. These transitions are known as ε-transitions.
  • q0 represents the start state.
  • F is a set of accepting states.

An NFA can be represented using a transition graph where the vertices correspond to states and the edges labeled with input characters represent transitions. An NFA accepts a string if and only if there is a path in the transition graph from the start state to one of the accepting states that matches the input string.

Epsilon Closure and the transition function

Before we start coding, we need to understand two important concepts: the ε-closure and the move operation.
The ε-closure of a state s in an NFA is the set of all states that can be reached from s by only epsilon transitions. It can also be defined for a set of states, let’s say S. In this case, the ε-closure of S is the union of the ε-closures of all individual states s in S.

For a set S and character c, move(S,c) is defined as the set of states reachable from the set of states S by consuming the input symbol c. In other words, move(S,c) = ∪(s∈S) move({s},c)

Implementation

Now, let’s start the exciting part: the implementation of the regex engine using all the concepts we’ve discussed so far.
First of all, let’s define C++ classes for state, NFA and the regex engine. Some of the functions are straightforward, so their names will clearly describe what they do.

1
2
3
4
5
6
7
8
9
10
11
12

class State
{
public:
    std::vector<State *> epsilonTransitions;
    std::map<char, std::vector<State *>> transitions;
    bool isAccepting;
    State(bool accepting = false) : isAccepting(accepting) {}
    void addEpsilonTransition(State *nextState);
    void addTransition(char c, State *nextState);
};

To simplify things, we’re using a separate vector to store all the epsilon transitions. transitions is a map, that stores input characters as keys and sets of states reachable from the current state as values. The variable isAccepting is set to true if the current state is an accepting state.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
class NFA
{
public:
    State *startState;
    State *acceptingState;
    std::vector<std::unique_ptr<State>> states;

    NFA()
    {
        std::unique_ptr<State> start = std::make_unique<State>();
        std::unique_ptr<State> accepting = std::make_unique<State>(true);
        startState = start.get();
        acceptingState = accepting.get();

        // transfer the ownership to the states vector
        states.push_back(std::move(start));
        states.push_back(std::move(accepting));
    }

    // transfers the ownership of the states of some NFA to the current NFA.
    void acquireStatesFrom(NFA &other);

    // functions for creating NFA using the McNaughton-Yamada-Thompson algorithm
    static NFA createForEpsilon();
    static NFA createForChar(char c);
    static NFA createForUnion(NFA &nfa1, NFA &nfa2);
    static NFA createForConcatenation(NFA &nfa1, NFA &nfa2);
    static NFA createForKleeneStar(NFA &originalNFA);

    static std::set<State *> epsilonClosure(const std::set<State *> &states);
    static std::set<State *> move(const std::set<State *> &states, char c);
};

Here, we’ve created the states vector for our convenience, as it will allow us to securely transfer ownership of states between NFAs later on. This is especially useful when implementing the McNaughton-Yamada-Thompson algorithm. Additionally, the vector manages the lifetime of the NFA states.

Construction of NFA using the McNaughton-Yamada-Thompson algorithm

This algorithm can be used to recursively convert any regular expression into an NFA that defines the same language. Although an NFA can have multiple accepting states, an NFA constructed using Thompson’s algorithm has exactly one accepting state. The accepting state cannot have any outgoing transitions. This means that once the NFA reaches the accepting state, it stops processing the input.

The algorithm defines NFA construction rules for the following base cases:

  1. Empty string (ε)

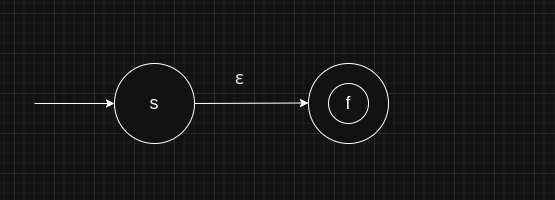
This is the NFA diagram for an empty string. A single circle represents a state, whereas concentric circles represent an accepting state. An arrow represents a transition from one state to another, given an input symbol. The ε-transition from the starting state s to the accepting state f accounts for no input symbols.

1
2
3
4
5
6
NFA NFA::createForEpsilon()
{
    NFA nfa;
    nfa.startState->addEpsilonTransition(nfa.acceptingState);
    return nfa;
}
  1. Literal a, where a ∈ Σ.
1
2
3
4
5
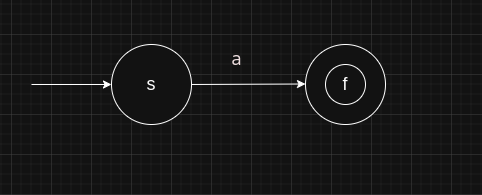
6
NFA NFA::createForChar(char c)
{
    NFA nfa;
    nfa.startState->addTransition(c, nfa.acceptingState);
    return nfa;
}

Now let’s create NFA for union, concatenation and Kleene closure. We’re gonna use ε-transitions a lot, as they allow the automaton move from one state to another without consuming any input character.

Union

Let r1 and r2 be two regular expressions, N(r1) and N(r2) be the corresponding NFA that define the language L. Then, the NFA of their union, N(r1|r2) can be represented by the following diagram.

1
2
3
4
5
6
7
8
9
10
11
12
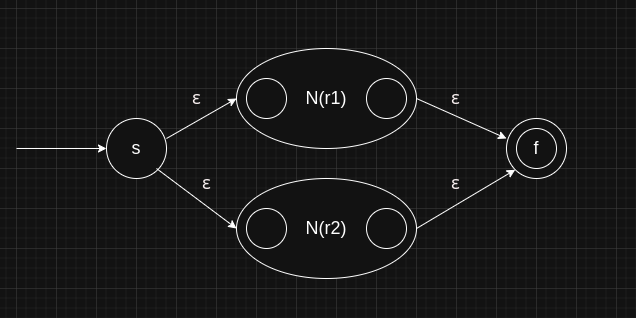
13
NFA NFA::createForUnion(NFA &nfa1, NFA &nfa2)
{
    NFA newNFA;
    nfa1.acceptingState->isAccepting = false;
    nfa2.acceptingState->isAccepting = false;
    newNFA.startState->addEpsilonTransition(nfa1.startState);
    newNFA.startState->addEpsilonTransition(nfa2.startState);
    nfa1.acceptingState->addEpsilonTransition(newNFA.acceptingState);
    nfa2.acceptingState->addEpsilonTransition(newNFA.acceptingState);
    newNFA.acquireStatesFrom(nfa1);
    newNFA.acquireStatesFrom(nfa2);
    return newNFA;
}

Concatenation

N(r1r2)

1
2
3
4
5
6
7
8
9
10
11
NFA NFA::createForConcatenation(NFA &nfa1, NFA &nfa2)
{
    NFA newNFA;
    nfa1.acceptingState->addEpsilonTransition(nfa2.startState);
    nfa1.acceptingState->isAccepting = false;
    newNFA.startState = nfa1.startState;
    newNFA.acceptingState = nfa2.acceptingState;
    newNFA.acquireStatesFrom(nfa1);
    newNFA.acquireStatesFrom(nfa2);
    return newNFA;
}

Kleene closure

The following diagram shows the NFA for kleene closure N(r*).

1
2
3
4
5
6
7
8
9
10
11
NFA NFA::createForKleeneStar(NFA &originalNFA)
{
    NFA newNFA;
    newNFA.startState->addEpsilonTransition(originalNFA.startState);
    newNFA.startState->addEpsilonTransition(newNFA.acceptingState);
    originalNFA.acceptingState->addEpsilonTransition(originalNFA.startState);
    originalNFA.acceptingState->addEpsilonTransition(newNFA.acceptingState);
    originalNFA.acceptingState->isAccepting = false;
    newNFA.acquireStatesFrom(originalNFA);
    return newNFA;
}

Parsing the Regex

Now that we have completed all the necessary setup for creating an NFA, all that needs to be done is to implement a parser. For that, we need to know the operator precedence of different regex operators. The operators (star, concatenation, and union) that we discussed in this post are all left-associative. The order of precedence from higher to lower is: Kleene star > concatenation > union. Before computing the Kleene closure, we must parse the atom, which could either be an epsilon or a character. Note that the regex can have parentheses as well, but we won’t be considering any operator precedence for them. Let’s create a class that will handle all this stuff for us.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class RegexEngine
{
public:
    RegexEngine(const std::string &regex) : pattern_(regex), pos_(0) {}
    void compile();
    bool matches(const std::string &target);

private:
    std::string pattern_;
    int pos_;
    NFA nfa_;

    NFA parseExpression();
    NFA parseUnion();
    NFA parseConcatenation();
    NFA parseStar();
    NFA parseAtom();
};

For this post, and to keep things simple, we’ll be writing a basic parser that uses recursive descent. There are other techniques, like Pratt parsing, that handle operator precedence very well, but we will not be discussing them in this post. We’ll be creating four functions: for parsing union, concatenation, Kleene closure, and atoms, respectively.

To handle operator precedence in recursive descent, we must ensure that functions corresponding to operators with lower precedence call the functions corresponding to operators with higher precedence i.e., higher precedence operators are parsed by functions that are called at deeper levels of recursion.

Note: To stay focused on the main objective of this post, we will not be dealing explicitly with move semantics or error handling. It will be done in the upcoming posts.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
// Recursive descent

NFA RegexEngine::parseUnion()
{
    NFA result = parseConcatenation();
    while (pos_ < pattern_.size() && pattern_[pos_] == '|')
    {
        pos_++;
        NFA nfaToMakeUnion = parseConcatenation();
        result = NFA::createForUnion(result, nfaToMakeUnion);
    }
    return result;
}

NFA RegexEngine::parseConcatenation()
{
    NFA result = parseStar();
    while (pos_ < pattern_.size() && pattern_[pos_] != '|' && pattern_[pos_] != ')')
    {
        NFA nfaToConcat = parseStar();
        result = NFA::createForConcatenation(result, nfaToConcat);
    }
    return result;
}

NFA RegexEngine::parseStar()
{
    NFA result = parseAtom();
    while (pos_ < pattern_.size() && pattern_[pos_] == '*')
    {
        pos_++;
        result = NFA::createForKleeneStar(result);
    }
    return result;
}

NFA RegexEngine::parseAtom()
{
    if (pos_ >= pattern_.size())
    {
        return NFA::createForEpsilon();
    }
    char curChar = pattern_[pos_++];

    // Move past the opening brace and get the NFA for the expression till a closing brace is found.
    if (curChar == '(')
    {
        NFA result = parseExpression();
        if (pos_ < pattern_.size() && pattern_[pos_] == ')')
        {
            // consume the closing brace
            pos_++;
        }
        else
        {
            std::cerr << std::format("Expected ), found {}\n", pattern_[pos_]);
            std::exit(1);
        }
        return result;
    }
    else
    {
        return NFA::createForChar(curChar);
    }
}

Now let’s create two wrapper functions.

1
2
3
4
5
6
7
8
NFA RegexEngine::parseExpression()
{
    return parseUnion();
}

void RegexEngine::compile(){
    nfa_ = parseExpression();
}

String matching

Now that we have our NFA, it is time to put it to real use. We want to find out whether a given string matches the regex. Recall that transitions from one state to another occur due to input characters. Also, recall that NFAs can have states with epsilon transitions, which we are allowed to follow freely without consuming any input. So, now it is the right time to handle the epsilon closure, which we discussed earlier. We want to find all the states that can be reached from the current state using only epsilon transitions.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
std::set<State *> NFA::epsilonClosure(const std::set<State *> &states)
{
    std::stack<State *> stateStack;
    std::set<State *> result = states;

    for (State *state : states)
    {
        stateStack.push(state);
    }

    while (!stateStack.empty())
    {
        State *currState = stateStack.top();
        stateStack.pop();
        for (State *next : currState->epsilonTransitions)
        {
            if (result.find(next) == result.end())
            {
                stateStack.push(next);
                result.insert(next);
            }
        }
    }
    return result;
}

This code computes the epsilon closure for a set of states, which is necessarily the union of the epsilon closures of each individual state within that set. An NFA is essentially a graph data structure, so standard graph algorithms like BFS (Breadth-First Search) and DFS (Depth-First Search) can be used to perform the traversal. In this case, we’ve used DFS. Please note that using a queue instead of a stack here would make it BFS.

Now let’s write the code for handling state transitions.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
std::set<State *> NFA::move(const std::set<State *> &states, char c)
{
    std::set<State *> result;
    for (State *state : states)
    {
        const std::map<char, std::vector<State *>> &transitionMap = state->transitions;
        if (auto itr = transitionMap.find(c); itr != transitionMap.end())
        {
            for (State *transition : itr->second)
            {
                result.insert(transition);
            }
        }
    }
    return result;
}

Now, let’s implement the function to determine whether a given string matches the regex pattern using the NFA.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
bool RegexEngine::matches(const std::string &target)
{
    std::set<State *> currentStates = NFA::epsilonClosure({nfa_.startState});

    for (char c : target)
    {
        currentStates = NFA::epsilonClosure(NFA::move(currentStates, c));
        if (currentStates.empty())
        {
            return false;
        }
    }
    for (State *state : currentStates)
    {
        if (state->isAccepting)
        {
            return true;
        }
    }
    return false;
}

A string matches a given pattern if there exists at least one valid path from the starting state of the NFA to its accepting state for that string. This function simulates the NFA execution by:

  1. Starting with all states reachable from the start state via epsilon transitions.
  2. For each character in the input string, finding the next possible states by applying the transition function to the current set of states with the current character, and then computing the epsilon closure of those resulting states to include all states reachable without consuming additional input characters.
  3. If at any point no valid states are found after processing a character, immediately returning false.
  4. After processing all characters, returning true if any of the current states is an accepting state.

Now that we’re done with everything, let’s test the code.

1
2
3
4
5
6
7
8
9
10
11
#include "engine.hpp"

int main(){
    std::string regex,input;
    std::cin>>regex>>input;
    RegexEngine re(regex);
    re.compile();
    bool res = re.matches(input);
    std::cout<<res<<std::endl;
    return 0;
}

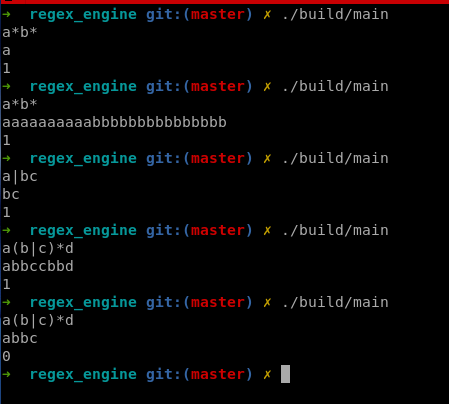
So, that’s all for this blog. Here, we learned how to build a basic regex engine using NFA. In the upcoming blogs in this series, we’ll explore DFAs and implement certain algorithms widely used in lexical analysis. We’ll also improve this code by adding certain optimizations and implementing proper error handling. The source code and tests can be found at https://github.com/0xsh4dy/regex_engine

References

  1. Aho, Alfred V., Monica S. Lam, Ravi Sethi, and Jeffrey D. Ullman. Compilers: Principles, Techniques, and Tools. 2nd ed. Pearson Education, 2006.

  2. https://www.cs.rochester.edu/u/nelson/courses/csc_173/fa/re.html